With large electronically steerable arrays, a picocellular base station can form narrow pencil beams toward a user, all but eliminating the probability of interfering with nearby transmissions. A critical challenge, however, is the agile adaptation of such large arrays to "track" mobile users, while accounting for frequently occurring blockages.
Existing mm-wave transceivers employ RF beamforming in place of per-element baseband control in order to simplify frontends, therefore classical least squares techniques are not applicable for channel estimation. The inherent sparsity of the mm-wave channel -- which consists of the LoS path and at most two or three reflections -- allows compressive channel tracking techniques with minimal (logarithmically scaling) overhead. 

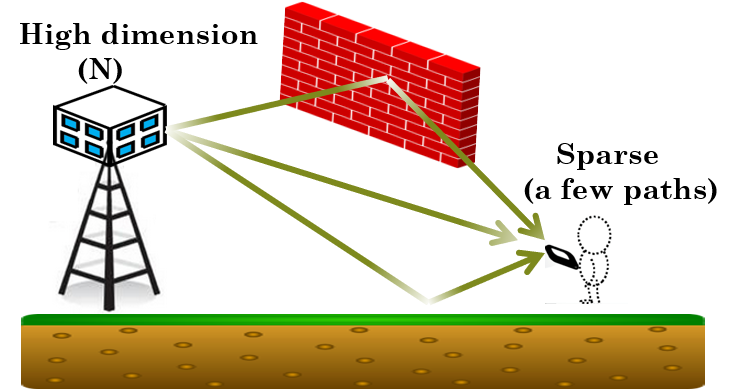
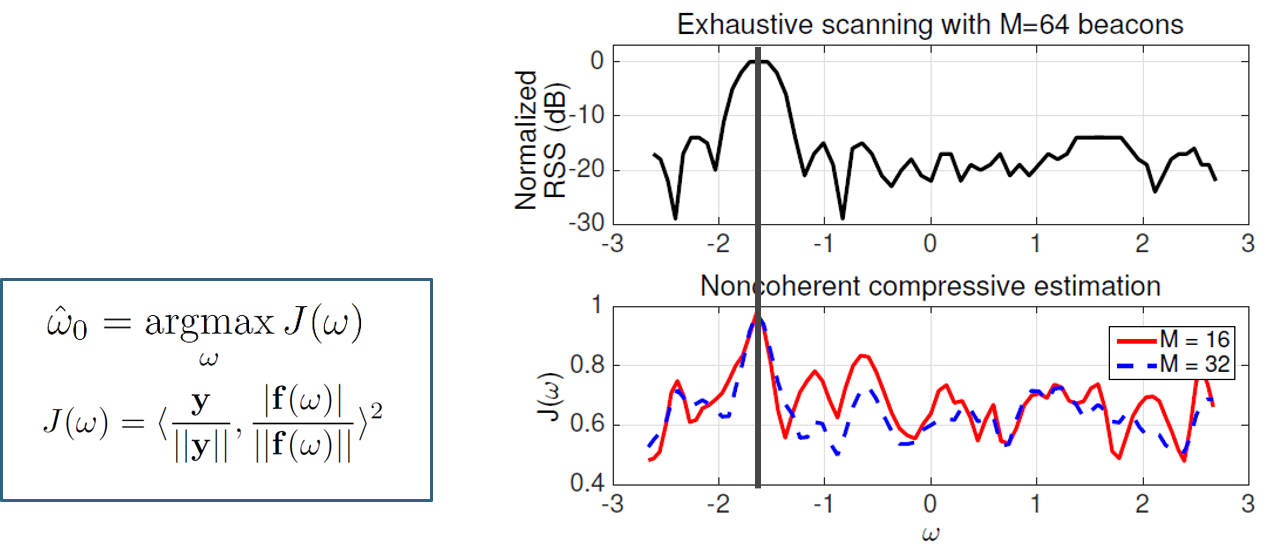
Since current mm-wave systems such as the 802.11ad standard are not designed to maintain phase coherence across packets, the phase information of compressive channel measurement can be corrupted. This motivates the development of a noncoherent compressive estimation framework that relies solely on received signal strength (RSS) measurements of compressive beacons.

For single-path channels (or channels with one dominant path), noncoherent template matching of the RSS measurement vector on an oversampled grid followed by Newton refinement is near-optimal at high SNR. We demonstrated this approach on a 16-element 60GHz phased array testbed provided by the facebook Terragraph team. This method is compatible with constrained (e.g., heavily quantized) beamforming weights and proves robust to noise and interference caused by weaker paths in the channel. Its main drawback is that it only recovers one (dominant) path.

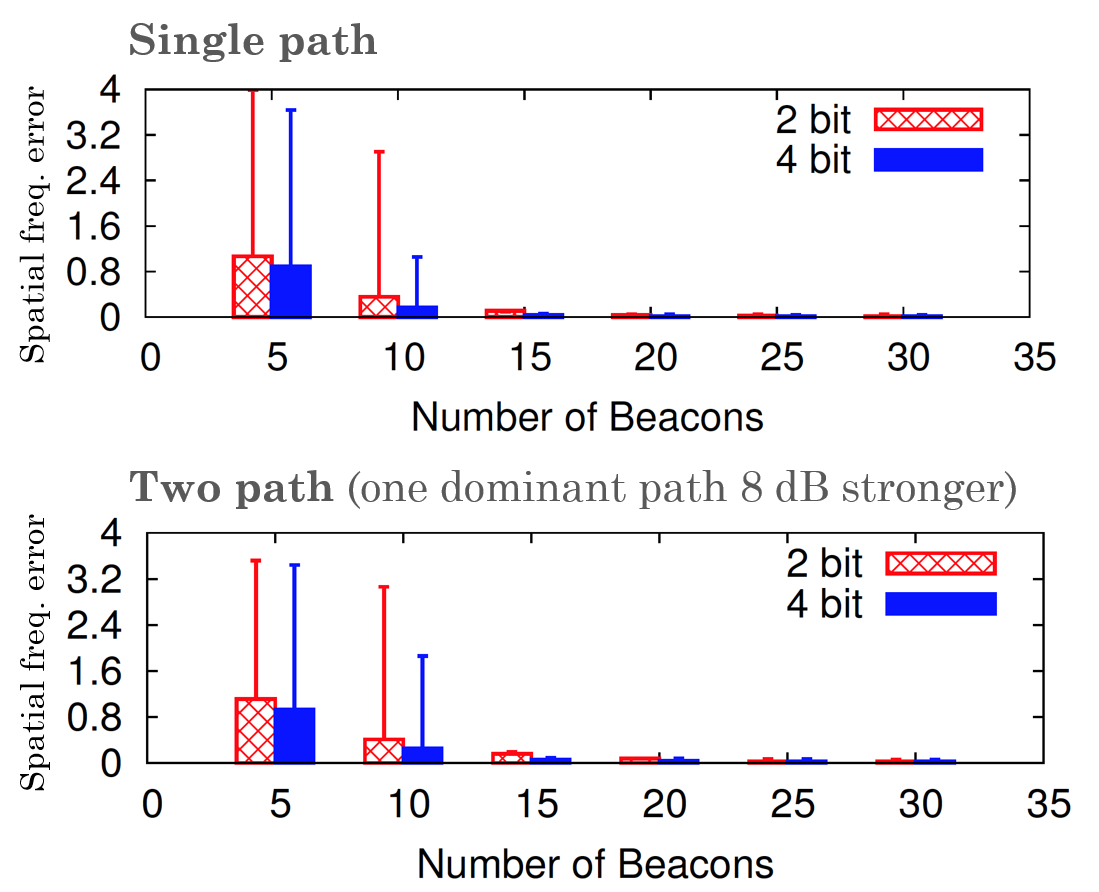
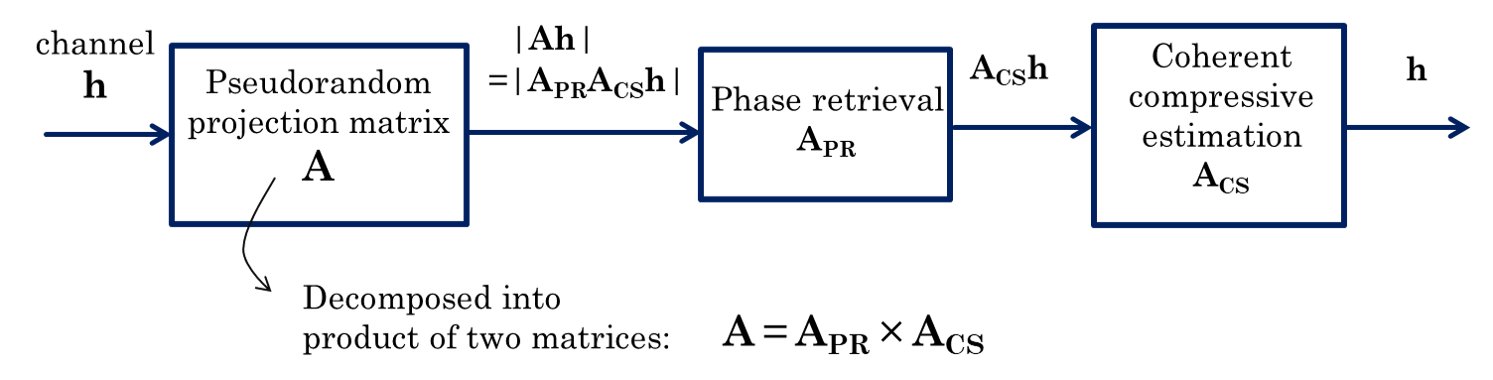
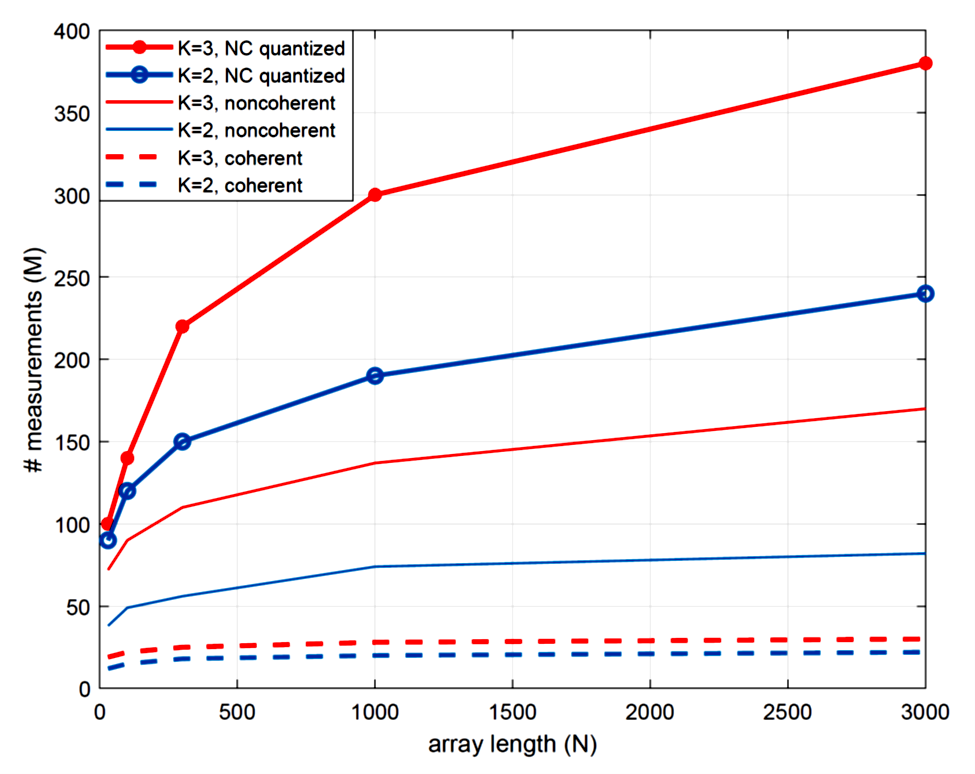
Since mm-wave links are susceptible to frequent blockage, it is very useful to track all viable paths in the channel so a backup path is ready when the strongest one is blocked. For tracking multipath channels, we proposed a two-stage algorithm which is a virtual concatenation of phase retrieval and compressive estimation with Newton refinements. This method is shown to scale logarithmically with array size and linearly with the number of paths, yet it is not easily adaptable to constrained beamforming weights. Developing alternative algorithms that are robust to hardware constraints is part of our ongoing research.