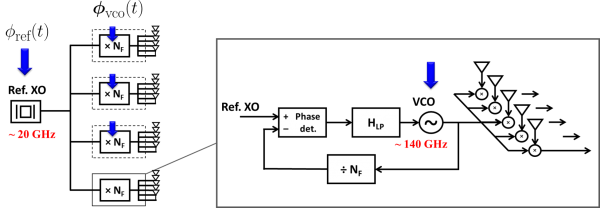
The small wavelength of mm-wave frequencies makes scaling to massive arrays of hundreds or thousands of elements possible even on small hand-held devices. In hardware, however, calibrating such a large frontend at RF frequencies is a daunting task. Modular architectures can be an effective approach to simplify scaling. 

The phased array antenna can be organized as an array of subarrays, with down-conversion and ADC performed on each subarray. This approach limits the transfer of RF signals to subarrays and digitized signals are conveyed to the centralized processor. To synchronize the entire array, a low frequency reference clock is distributed to subarrays and frequency multiplication is performed on each subarray to obtain the RF reference. Fig. 1 depicts this process. 

The system shown in Fig. 1 is affected by phase noise generated in the reference oscillator as well as independent phase noise terms generated at each of the on-tile VCO's used for frequency multiplication. The over all phase noise at each antenna element is a combination of the reference noise and the VCO phase noise of its respective tile VCO. Applying the linearized PLL model, the former is low-pass filtered and the latter is high-pass filtered by the PLL in the process of frequency multiplication. 

Assuming phase drift is tracked at the output of the LMMSE receiver for callibrating the symbol constellation, the low-pass reference phase noise is tracked and corrected leaving the high-pass filtered VCO noise as the dominant source of distortion. Since the VCO noise is independent across tiles and the LMMSE receiver uses a combination of elements on all tiles to produce the output of each channel, the output phase noise is effectively the average of tile phase noise terms, and thus a factor of N_T weaker in PSD than the filtered VCO noise. This means tiling can actually be beneficial and allow us to use noisier PLL's. 

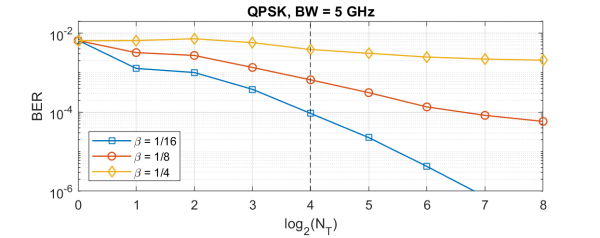
Uncorrelated phase noise across elements also leads to cross-talk interference between channels. The strength of this interference term is proportional to the loading factor - the ratio of number of users (channels) to array size. This means that by maintaining a fixed loading factor and tile size, it is possible to scale to large number of users and array size with modest VCO phase noise requirements. Fig. 2 shows the average bit error rate of channels for a 256-element array as a function of number of tiles (for each point on this graph, the tile size is 256/#tiles).